更新日: 2020/11/05
感染症治療薬ジスロマックの通販。価格比較や最安値サイトを紹介。
ジスロマックの通販価格と最安値サイト

ジスロマックは、クラミジアや淋病などの治癒率90%前後の感染症治療薬です。
病院でも処方されているため安全性が高く、クラミジア治療なら最短10日での完治が期待できます。

ここでは、感染症治療薬のジスロマックの通販価格や最安値サイト、クラミジアの検査が自宅でできる検査キットなどを紹介しています。
| サイト |  ライフパートナー |
 お薬なび |
 グー薬局 |
 メデマート |
|---|---|---|---|---|
| 【6錠入り】 250㎎ |
3,150円 (1錠/525円) |
3,150円 (1錠/525円) |
3,150円 (1錠/525円) |
3,150円 (1錠/525円) |
| 【18錠入り】 250㎎ |
8,980円 (1錠/498円) |
8,980円 (1錠/498円) |
8,980円 (1錠/498円) |
8,980円 (1錠/498円) |
| 【30錠入り】 250㎎ |
14,180円 (1錠/472円) |
14,180円 (1錠/472円) |
14,180円 (1錠/472円) |
14,180円 (1錠/472円) |
| 購入 | 【ライフパートナー】 ジスロマックの購入ページへ |
【お薬なび】 ジスロマックの購入ページへ |
【グー薬局】 ジスロマックの購入ページへ |
【メデマート】 ジスロマックの購入ページへ |
ジスロマック250㎎を取り扱っている通販サイトは多くはなく、今回紹介しているサイトでは全て同じ価格でした。
そのため、購入するポイントとしては、各サイトごとの割引やキャンペーンなどを比べて、購入すると良いでしょう。
【約20分で検査ができる】クラミジア検査キット
ジスロマックを通販購入する場合は、一緒にクラミジア検査キットの購入がオススメです。
クラミジア検査キットは、自宅で簡単に検査することができ、約20分で検査結果を知ることができます。

病院に行きづらい方や時間がない方は、事前にクラミジア検査キットを購入しておくと感染状態がいつでも確認できます。
| サイト |  ライフパートナー |
 お薬なび |
 グー薬局 |
 メデマート |
|---|---|---|---|---|
| 3回分 | 3,150円 | 3,150円 | 3,150円 | 3,150円 |
| 購入 | 【ライフパートナー】 クラミジア検査キット |
【お薬なび】 クラミジア検査キット |
【グー薬局】 クラミジア検査キット |
【メデマート】 クラミジア検査キット |
この記事の目次
ジスロマックの口コミ

ジスロマックの口コミを紹介します。
杏さん(28歳)
安心して飲むことが出来ましたし、たった3日間忘れずに飲むだけで、ちゃんと治りました
参照:https://okusurinavi.shop/prd_review.php?pid=471#item_review
ジスロマックは主にクラミジア治療で利用している方がほとんどですが、歯周病や風邪、扁桃炎などにも効き目のある治療薬です。

幅広い症状の改善が期待できるため、常備薬として切らさないようにしている方も多いようです。
ジスロマックの取り扱いサイト
ここでは、ジスロマックを取り扱っている通販サイトを紹介します。
| サイト |  ライフパートナー |
 お薬なび |
 グー薬局 |
 メデマート |
|---|---|---|---|---|
| 運営年数 | 12年 | 11年 | 2年 | 4年 |
| 利用者数 | 11万人以上 | 100万人以上 | 急増中 | 増加中 |
| 決済方法 |
クレジット 銀行振込 コンビニ |
クレジット 銀行振込 コンビニ |
クレジット 銀行振込 コンビニ |
クレジット 銀行振込 コンビニ |
| お得情報 | 割引・ポイント還元 | 初回限定500割引 | 初回限定500割引 | 初回限定500割引 |
| 購入 | 【ライフパートナー】 公式サイト |
【お薬なび】 公式サイト |
【グー薬局】 公式サイト |
【メデマート】 公式サイト |
ライフパートナーのお得情報

■商品代金5%OFF + ポイント5%還元
・条件:銀行振込
・内容
【ジスロマック250㎎:18錠/8,980円】
を購入した場合
銀行振込で5%OFF
8,980円 - 449円(5%OFF) = 8,531円
ポイント5%還元
449円分のポイント付与
銀行振込にすることで898円の割引が適応され、送料(1,000円)がほぼ無料になります。
>>ジスロマックの取り扱いサイトに戻る
お薬なびのお得情報

■初回限定500割引クーポン
初回購入から使用できるクーポン。
クーポンコード:Syokai500
■【銀行振込限定】5%OFF + 5%還元
条件:現行振込
内容:商品代金5%OFF+5%還元
>>ジスロマックの取り扱いサイトに戻る
グー薬局のお得情報

■初回限定500割引クーポン
初回購入から使用できるクーポン。
クーポンコード:GOOD500
■【銀行振込限定】5%OFF + 5%還元
条件:現行振込
内容:商品代金5%OFF+5%還元
>>ジスロマックの取り扱いサイトに戻る
メデマートのお得情報

■初回限定500割引クーポン
初回購入から使用できるクーポン。
クーポンコード:Syokai
■レビュー投稿で300PTキャッシュバック
商品を注文後、商品レビューを投稿すると、300PT(300円)がキャッシュバック
>>ジスロマックの取り扱いサイトに戻る
ジスロマックで治療できる感染症
ジスロマックで治療できる症状をまとめています。
主にクラミジアや淋病、歯周病などの治療で使用されることが多いジスロマックですが、他にも多くの症状に有効な抗生物質です。
- 尿道炎(クラミジア・淋病など)
- 子宮頚管炎
- 咽頭炎
- 副鼻腔炎
- リンパ管炎
- 扁桃炎
- 気管支炎
- 歯周病
- 肺炎
幅広い症状の治療に使用されるジスロマックですが、特にクラミジアと歯周病には非常に高い有効性があります。
クラミジアの治療期間
クラミジアの治療期間の目安は以下の通りです。

クラミジアは正しく治療すれば、1週間程度で治療できる感染症です。
女性の場合、約80%は無症状ですが、男性は日が経つにつれて、痒みから痛みへと変化するので、おかしいと感じたら早期に検査・治療を行いましょう。
クラミジアの検査キットは通販サイトで購入できるので、事前に手元に置いておくとすぐに感染状態を知ることができます。
通販でジスロマックを購入した際も、同時に検査キットの購入すると病院で検査をする必要もなくなります。
再検査で陽性が出てしまった場合
クラミジア治療の開始から3週間後に検査をしたが、再度陽性反応が出てしまった場合は、もう一度ジスロマックを服用しましょう。
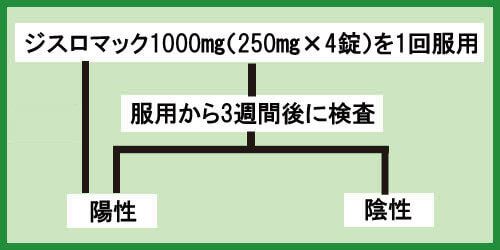
用量や飲み方はこれまでと同じです。
ジスロマック1000㎎(250㎎×4)1回
その後、3週間後に再検査を行ってください。
ジスロマックの飲み方

ここでは、ジスロマックの飲み方について紹介しています。
ジスロマックは幅広い症状に有効ですが、症状に応じて飲み方が異なるので注意しましょう。
【性感染症】
クラミジア・淋病など(尿道炎・子宮頚管炎)
ジスロマック1000㎎(250㎎×4)を1回服用
【性感染症ではない場合】
歯周病・風邪などの症状
ジスロマック500㎎(250㎎×2)を1日1回3日間服用
以下のリンク先では、ジスロマックの服用方法の注意点などを詳しく説明しています。
ジスロマックの副作用
ジスロマックの副作用について紹介しています。
- 下痢
- 胃が痛い、腹痛
- 吐き気
- 眠気
- 湿疹(発疹)、痒み
- 発熱
- 頭痛
以下のリンク先では、【ジスロマックの副作用】について詳しく説明しています。
ジスロマックが服用できない方
以下のような方はジスロマックの服用ができません。
・有効成分アジスロマイシンに過敏症の反応がでる方
・他のマクロライド系またはケトライド系薬剤に対し過敏症の既往歴のある方
┗マクロライド系:エリスロシン、クラリス、クラリシッドなど
┗ケトライド系:セスロマイシン、ソリスロマイシン
・肝臓機能に障害のある方
・心疾患のある方
・授乳中の方
ジスロマックの注意点
以下の項目から知りたい注意点をクリックしてください。
【ジスロマックの飲み合わせ】
ジスロマックの飲み合わせを解説!ロキソニンやピルとの相性は?

【ジスロマックとアルコール】
ジスロマックの飲み合わせを解説!ロキソニンやピルとの相性は?

【ジスロマックと下痢の症状】
ジスロマックを服用してから飲酒OKになるまでの期間や、服用中にお酒を飲んでしまったときの対処法などを紹介。
ジスロマックの良くある質問
ここでは、ジスロマックに関するよくある質問をまとめています。
■クラミジアの再検査は必ずするべきですか?
再検査は必ずするべきです。
万が一、完治できていない場合、パートナーに移してしまったり、治まっていた症状が悪化してしまう場合があります。
忙しい方は、通販サイトでもクラミジアの検査キットの購入ができるので、治療後は必ず再検査を行いましょう。
■検査はいつやったらいいですか?
クラミジアの再検査は、治療を初めてから3週間後になります。
3週間より前に検査してしまうと、菌の死骸などの影響で陽性になってしまう可能性があります。
例)
治療開始日:11/1(1000㎎を1回服用)
再検査日:11/22~
■パートナーをクラミジアに感染させてしまったかもしれない場合
パートナをクラミジアに感染させてしまった疑いがある場合は、早期に検査を行いましょう。
また、パートナーも感染していた場合は、必ず一緒に治療を行い、ピンポン感染を予防しましょう。
女性に感染させてしまった場合、無症状の方が多く、感染に気付かないことがあり、放っておくと最悪不妊症や流産などの原因になります。
男性に感染させてしまった場合は、尿道の痒みや痛みが伴います。
※ピンポン感染…パートナー間で感染させあっている状態。自身が完治しても再度パートナーから感染してしまう状態。
【クラミジア】数日間症状はおさまっていたのに、突然緑っぽいおりものがでてきた。
再発の可能性も考えられるため、一度検査をするのがいいでしょう。
忙しい方や病院に行く時間がないという方は、通販サイトでも検査キットが購入できるのでそちらをお勧めします。
■ジスロマックはクラミジア以外にどんな感染症に有効ですか?
ジスロマックはクラミジア以外に、以下のような症状に有効です。
・扁桃炎
・抜歯後の化膿止め
・尿道炎
・マイコプラズマ肺炎
・咽頭炎
・歯周病
上記は、ジスロマックが有効な代表的な症状です。
それ以外にも、幅広い感染症に利用されています。
ジスロマックは個人輸入がお得

ジスロマックを手に入れるには、病院で処方してもらうか通販で購入する必要があります。

病院では、待ち時間や通院、診察料がかかるため、通販にくらべ時間と治療費が大きくなってしまいます。

また、クラミジアなどの症状であれば保険適応外となる場合もあり、大きな出費となる可能性もあります。

通販サイトの場合は、診察代や検査費用などもないので、薬代と送料のみでジスロマックが購入できます。
以下では、1ヶ月にかかるクラミジアの治療費用を病院と通販で比べてみました。
| 合計金額 | 内訳 | |
|---|---|---|
| 病院 | 25,000円~ | ジスロマック(1回分/2~4錠)15,000円 検査費用(1回)8,000~10,000円 |
| 通販 | 約7,350円 | ジスロマック(6錠)3,150円 検査キット(3回分)3,150円 送料0~1,000円 |
通販を利用することで1ヶ月約7,350円でジスロマックが購入できます。
通販サイトでも服用方法や副作用は詳しく説明されていますが、医師から指導がある方が安心な方は病院がおすすめです。
ジスロマックは市販では購入できない

ジスロマックは風邪や扁桃炎、クラミジアなどに有効な便利な医薬品ですが、ドラッグストアなどでは市販されていません。
ジスロマックは国内では処方箋が必要な医薬品のため、市販ができなくなっています。
しかし、個人輸入代行サイトで通販する場合は海外から取り寄せるので、病院と同じ医薬品を処方箋なしで手に入れることができます。
Amazon・楽天でも通販できない

ジスロマックはAmazon・楽天などの国内の通販サイトでの購入はできません。
Amazon・楽天などの一般的な通販サイトでは、基本的に病院処方薬などの医薬品は取り扱えないので、ジスロマックを通販する際は個人輸入代行サイトを利用することになります。
ジスロマックを通販でお得に購入しよう

ジスロマックは、幅広い症状に有効な医薬品ですが、病院で処方してもらうと高額な費用が掛かってしまいます。
しかし、個人輸入代行サイトであれば、費用を抑えながらジスロマックを購入することができます。
特にクラミジアの場合は、病院では保険適応外になる可能性もあり、高額な治療費がかかることもあります。
通販は注文から届くまでに約2週間程度かかってしまいますが、治療費をながらクラミジアや淋病などの感染症の治療が行えます。
| サイト |  ライフパートナー |
 お薬なび |
 グー薬局 |
 メデマート |
|---|---|---|---|---|
| 【6錠入り】 250㎎ |
3,150円 (1錠/525円) |
3,150円 (1錠/525円) |
3,150円 (1錠/525円) |
3,150円 (1錠/525円) |
| 【18錠入り】 250㎎ |
8,980円 (1錠/498円) |
8,980円 (1錠/498円) |
8,980円 (1錠/498円) |
8,980円 (1錠/498円) |
| 【30錠入り】 250㎎ |
14,180円 (1錠/472円) |
14,180円 (1錠/472円) |
14,180円 (1錠/472円) |
14,180円 (1錠/472円) |
| 購入 | 【ライフパートナー】 ジスロマックの購入ページへ |
【お薬なび】 ジスロマックの購入ページへ |
【グー薬局】 ジスロマックの購入ページへ |
【メデマート】 ジスロマックの購入ページへ |
