梅毒は初期段階での発見と治療が大切
梅毒セルフチェック
更新日:2020/02/28
梅毒はキスやセックスをする事で感染する性感染症です。病原菌「トレポネーマ」に感染することによって引き起こされ、第1期→第2期・・・と、4つの段階を経て症状が進みます。
一旦症状が出ても放置しておけば症状が治まるため、治ったと勘違いする方も多いですが、薬で治療しない限り感染は継続しています。治療しないまま放置すると最後は死に至る事もあるので、感染が疑われる時は必ず検査する事をオススメします。
通販なら梅毒に感染しているかどうかセルフチェックを行う事のできるキットを購入する事ができます。病院で検査するよりも安く済むので忙しい方や他人に知られたくないという方にオススメです。
| 病院での検査 | 2,000~8,000円(検査料のみ) |
| 通販 | 2,850円(検査キット代のみ) |
もし自宅で検査キットを使って検査した結果、梅毒に感染している「陽性反応」が出てしまった場合はすぐに病院へ行って薬を出してもらうか、梅毒に効果のあるペニシリン系の「アモキシシリン」という抗生物質を通販で購入する事をオススメします。
・小さなしこり
・股の付け根の部分(鼠径部)のリンパ節の腫れ
アモキシリン 1日500㎎を3回、2~4週間
・バラ疹や梅毒性丘疹
・粘膜疹と呼ばれる湿疹の症状
アモキシリン 1日500㎎を3回、4~8週間
これらの症状は何もしなくてもしばらくしたら治ってしまいますが、梅毒には感染したまま感染の次の段階へ進んでしまうので、陽性反応が出た場合はかならず治療を行って下さい。
ここのページで知りたい事
梅毒の感染ルート

梅毒は「トレポネーマ」という細菌によって引き起こされ、粘膜や皮膚の接触によって感染します。
主な感染ルートは性行為によるもので、性器と性器が接触する通常のセックスの他にも、アナルセックスやオーラルセックスでも感染します。キスでも感染する事があるので注意が必要です。
また妊娠している女性が梅毒に感染すると、胎盤や産道を通して赤ちゃんに感染する事もあります。このようにして赤ちゃんに感染する梅毒は先天性梅毒と呼ばれており、非常に重い障害を赤ちゃんに残してしまいます。
梅毒はじわじわと増えている!

日本では2010年頃から梅毒の感染者数が増加傾向にあります。
2017年には44年ぶりに5,000人を超えたと報告されており、社会的な問題になりつつあります。
感染初期は症状が目立たない事も多いので、潜在的な感染者数はもっと多いのではないかと推測されています。
初期段階の症状が現れても、女性は約半数、男性は3人に1人は気がつかないと言われています。梅毒にかかっている人と性行為を1回行うと約3分の1という高確率で感染するので、本人も周りの人も知らない間に梅毒はどんどん感染を広げてしまいます。
梅毒の症状
梅毒の症状は4つの段階を経て進行します。第1期と第2期までなら適切な治療で完治する可能性が高いですが、第3期、第4期にまで症状が進むと重い後遺症が残ります。
第1期
感染から約3週間~3ヵ月が経過した時期の事を言います。感染した部分(口の中や唇、陰部)に痛みを伴わないしこりができます。脚の付け根のリンパ節が腫れる事もあります。
いずれの症状も自然になくなってしまいますが、病原菌は体の中に潜んでおり、他の人に感染する可能性があります。
第2期
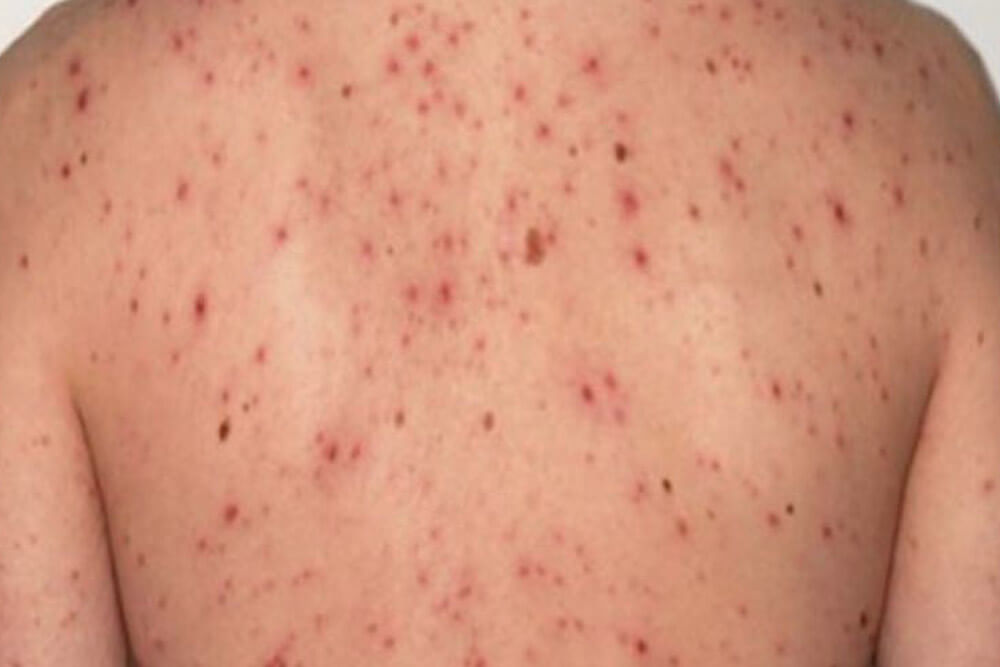
感染から約3ヵ月~3年が経過した時期です。全身のリンパ節の腫れ、倦怠感、発熱、関節痛等の症状が出る事があります。
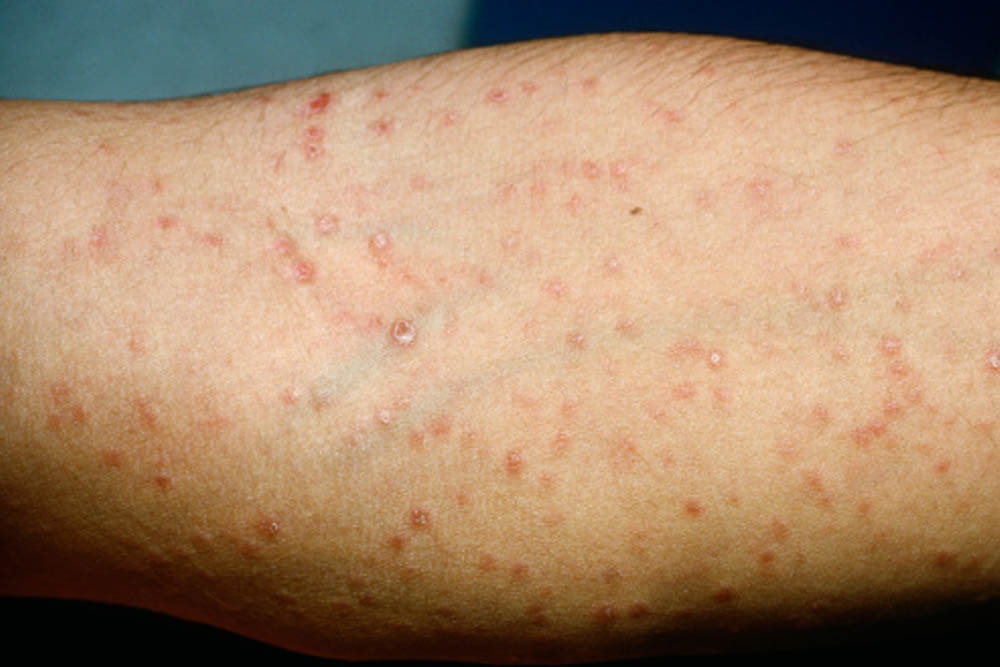
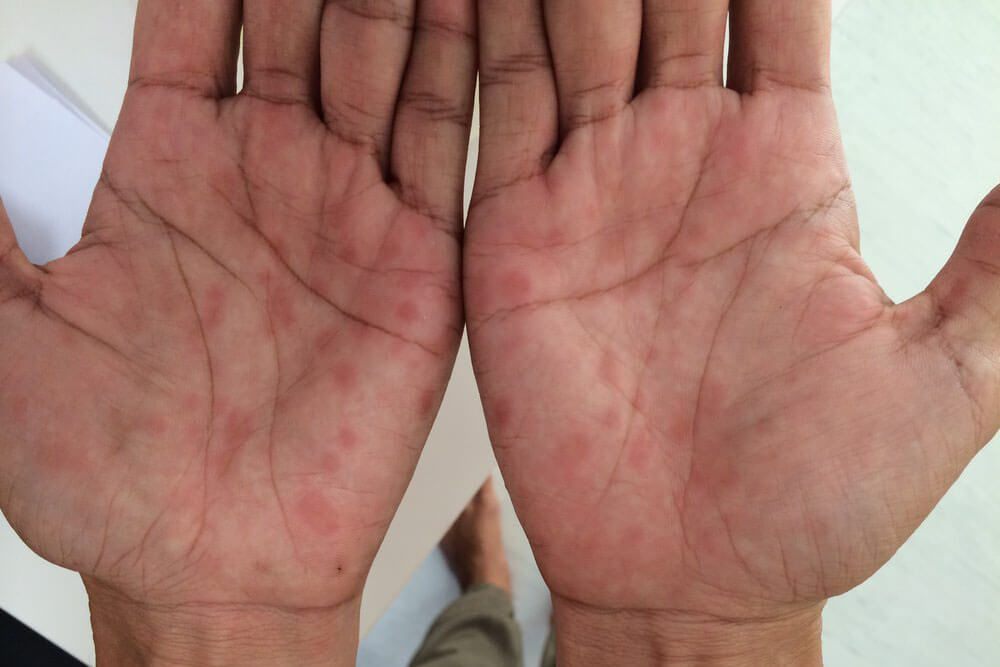
梅毒を代表する「バラ疹」と呼ばれる赤い発疹が手足の裏から全身、顔面へと広がります。
これらの症状も治療しなくても約1ヵ月ほどで消えますが、抗生物質による治療が行われない限り病原菌は体内に残ります。
アレルギーや風疹、はしかに間違われる事もあります。
第2期ではバラ疹も含めて、他に以下のような症状が現れます。
バラ発疹
痛みも痒みも伴いませんが、頭皮に発疹が生じると髪の毛が虫食い状態に抜け落ちる事があります。
扁平コンジローマ
脇の下、陰部、肛門等の柔らかくて湿った部分に平らで滑らかな腫れものができます。破れて体液が染み出る事があり、にじみ出た分泌物には多くの病原菌が含まれているので、皮膚の接触によって簡単に梅毒がまき散らされてしまいます。
肝炎
肝臓に梅毒が拡がって腹痛や黄疸(皮膚や白目が黄色になる)が起こり、尿が濃くなります。
その他
梅毒は血液を通して全身に広がるので、脳や目、耳に感染して頭痛や視力・聴力・平衡感覚の障害を引き起こす事もあります。
第2期の症状が消えると同時に長い潜伏期間に入り、この期間が始まってから2~3年の間は症状が再発する事もあります。
潜伏期間は数年~数十年に及ぶ場合もあり、やはり治療をしない限り病原体は残り続けます。
第3期
感染から約3~10年が経過した時期です。骨や筋肉、皮膚にゴムのような腫瘍(ゴム種)が発生し、外見上の後遺症を残します。
骨にできたゴム種は激痛を引き起こします。
第4期(末期)
感染から10年以上経過した時期です。多数の臓器、脳や神経が侵され、運動機能や知能に後遺症を残します。
排泄のコントロールすらできなくなる事があり、最悪の場合、死に至ります。
先天性梅毒
胎盤や産道を介して母親から赤ちゃんへ感染する先天性梅毒は、生後数年までに肺炎、肝臓や膵臓の増大、神経症状、発熱、発疹が現れます。
妊娠16週から20週以前に母体側の梅毒をきちんと治療すれば胎児への感染は予防できるとされています。治療がされない場合、赤ちゃんに重篤な後遺症を残します。
梅毒の検査方法

梅毒は血液検査によって診断されます。第一期の初期は感染していても検査で陽性反応が出ない場合があるので、感染から約3週間以上経過してからの検査が推奨されています。
男性の場合は泌尿器科や性病科、女性の場合は性病科や産婦人科で受診します。地域によっては保健所において匿名・無料で検査を受けられるところもあります。
検査のための時間が取れない、絶対に知人等に知られたくないという場合は後ほど詳しく説明しますが、自宅で検査を行える検査キットも販売されています。
梅毒の治療方法

一般的に梅毒は梅毒を殺すペニシリン系の抗生物質の服用によって治療します。薬は梅毒が体から確実にいなくなるまで服用する必要があります。
治療中は性行為等の感染につながる行為を避けましょう。性的な関係を持っているパートナーがいる場合は一緒に検査を受けてもらい、梅毒に感染しているようなら一緒に治療を受けるようにしましょう。
梅毒は何度でも感染してしまう性病なので、互いにきちんと治療しておかないと再感染を繰り返してしまいます。
梅毒検査と治療は自宅で可能!
「梅毒に感染したかどうか心配だけれど、病院へ行く時間が取れない」
「絶対に通院しているところを知っている人に見られたくない」
梅毒は検査と治療が必須だとわかっていても、上記のような理由で病院へなかなか足を運べない人が多いのではないでしょうか。
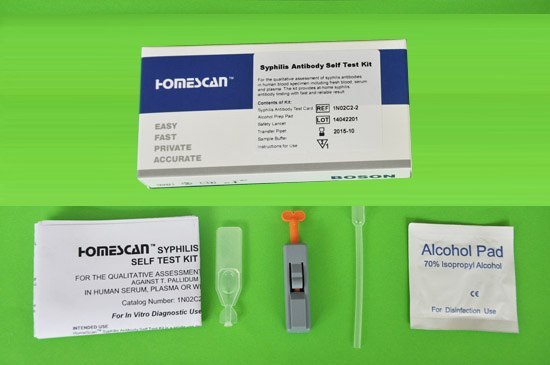
そんな人には自宅で簡単にできる検査キット「梅毒セルフテスト」がおすすめです。
約20分という早さで検査結果を得られるので、不安な気持ちで結果を待つ時間が短くて済みます。
梅毒セルフテストは個人輸入代行サイトの通販で購入できます。
梅毒セルフテストの使い方
梅毒セルフテストは以下の手順で使用します。
①付属のパットで指先や指回りを消毒する
②ランセット(使い捨ての針)を消毒した指の腹に当ててボタンを押す
③血が出るのでスポイトを使って採血
④テストカードの『S』の部分に血を垂らす
⑤さらに『S』の部分に検査液を垂らす
⑥約20分待つ
検査結果は2本の線が出たら陽性(梅毒確定)です。
梅毒は感染によって免疫がつく事はなく、何度でも感染する可能性があります。
通販ではまとめ買いで梅毒セルフテストがさらにお買い得になるので、今後の感染が心配な方は保険として複数購入してはいかがでしょうか。
1個・・・2,850円
2個・・・5,130円(1個あたり2,565円)
6個・・・13,680円(1個あたり2,280円)
梅毒セルフテストと同じように梅毒治療薬『アモキシシリン』もまとめ買いがお得です。
下記に通販の価格表を載せたので、薬を注文する際に参考にしてください。
21錠・・・1,420円(1錠あたり67円)
63錠・・・3,830円(1錠あたり60円)
105錠・・・5,680円(1錠あたり54円)
21錠・・・1,900円(1錠あたり90円)
42錠・・・3,420円(1錠あたり81円)
63錠・・・4,560円(1錠あたり72円)
梅毒は完治するの?
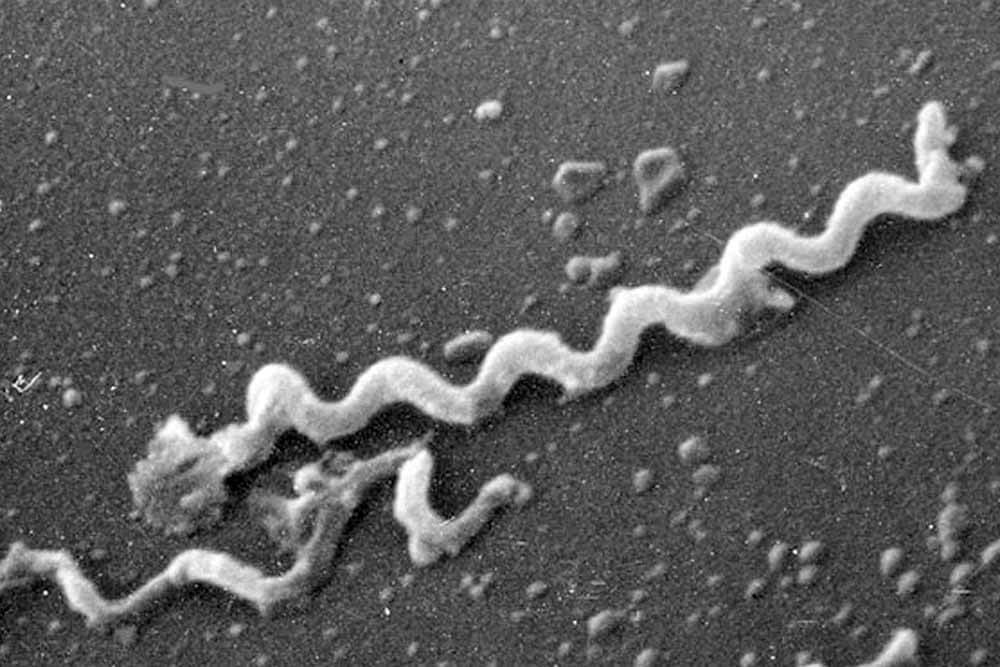
梅毒は一度感染したら治らない、という事をよく聞きますが、実際のところどうなのでしょうか?
結論から言うと、梅毒は初期の頃に正しく治療すれば完治できます。
「え?でも梅毒の完治は不可能だってよく聞くけれど・・・」
確かにネット上では梅毒は完治不可能という情報をいたる所で見かけます。
しかし、これは『大半は』正しくない情報で、梅毒初期の頃に抗生物質を正しく服用すれば完治が可能なのです。
ここで『大半は』を強調した理由は、治療が遅れると完治しない事もあるからです。
梅毒は感染から時間が経てば経つほど、体からトレポネーマを完全に殺す事が難しくなります。
また、第三期や第四期の段階まで重症化すると治療しても後遺症が残ってしまいます。
放っておいて治ったように見えても、自然治癒する事はないので、手遅れになるまで何度でも症状が再発します。
一度感染して完治すると、もう梅毒にならないだろうと甘く見る人がいますが、梅毒は免疫がつかないので予防を怠っていると再度梅毒に感染してしまいます。
再感染する可能性がある、という事実が梅毒は完治しないという誤った認識を生み出している事も考えられます。
梅毒は早期に治療を開始して、完治したらもう二度と罹患しないためにもしっかりと予防しましょう。
治療薬はトレポネーマを完全に殺すために、病原菌がいなくなるまで飲み続ける必要があります。
梅毒予防のために必ずコンドームを着ける
梅毒は感染した部分と皮膚や粘膜が触れる事によって感染するので、予防にはコンドームの使用が有効です。
通常の性行為の他にも、オーラルセックスやアナルセックスのときにも使用する事をおすすめします。
しかしコンドームに覆われていない部分の皮膚や、キスでも感染の可能性があるので、コンドームによる100%の予防は残念ながら不可能です。
コンドームをあまり過信せずに、少しでも梅毒と思われる症状が見られたら、早めの検査治療を行ってください。
梅毒は早めの検査と治療が大切!

梅毒は恐ろしい病気ですが、感染初期の頃に適切な治療を受ければ完治可能です。
「梅毒が心配だけれど病院に行くのは気が引ける・・・」
そう自分に言い訳をして検査や治療を先延ばしにすると、待っているのは悲惨な結末です。
梅毒は自宅で検査も治療もできます。病院に行くのがためらわれるようなら通販で検査キットと治療薬を購入しましょう。
早期発見と早期治療があなたの未来を救います。